Статистика - Нормальное распределение

Нормальное распределение является важным распределением вероятностей, используемым в статистике.

Многие реальные примеры данных имеют нормальное распределение.

Нормальное распределение

Нормальное распределение описывается средним (\(\mu\)) и стандартным отклонением (\(\sigma\)).

Нормальное распределение часто называют "колоколообразной кривой" из-за его формы:

• Большинство значений около центра (\(\mu\))
• Медиана и среднее значение равны
• У него только один режим
• Он симметричен, то есть уменьшает на одинаковую величину слева и справа от центра.

Площадь под кривой нормального распределения представляет вероятности для данных.

Площадь под всей кривой равна 1, или 100%

Вот график нормального распределения с вероятностями между стандартными отклонениями (\(\sigma\)):

• Примерно 68.3% данных находится в пределах 1 стандартного отклонения от среднего (от μ-1σ to μ+1σ)
• Примерно 95.5% данных находится в пределах 2 стандартных отклонений от среднего (от μ-2σ to μ+2σ)
• Примерно 99.7% данных находится в пределах 3 стандартных отклонений от среднего (от μ-3σ to μ+3σ)

Различные средние и стандартные отклонения

Среднее значение описывает, где находится центр нормального распределения.

Вот график, показывающий три разных нормальных распределения с одинаковым стандартным отклонением, но разными средними значениями.

Стандартное отклонение описывает, насколько распространено нормальное распределение.

Вот график, показывающий три разных нормальных распределения с одинаковым средним, но разными стандартными отклонениями.

У фиолетовой кривой наибольшее стандартное отклонение, а у черной кривой наименьшее стандартное отклонение.

Площадь под каждой кривой по-прежнему равна 1, или 100%.

Пример нормально распределенных данных на реальных данных

Реальные данные часто распространяются нормально.

Вот гистограмма возраста лауреатов Нобелевской премии, когда они выиграли эту премию:

Нормальное распределение, нарисованное в верхней части гистограммы, основано на среднем значении генеральной совокупности (\(\mu\)) и стандартном отклонении (\(\sigma\)) реальных данных.

Мы видим, что гистограмма близка к нормальному распределению.

Примеры реальных переменных, которые могут иметь нормальное распределение:

• Результаты тестов
• Высота
• Вес при рождении

Распределение вероятностей

Распределения вероятностей - это функции, которые вычисляют вероятности исходов случайных величин.

Типичными примерами случайных величин являются подбрасывание монет и костей.

Вот график, показывающий результаты растущего числа подбрасываний монет и ожидаемые значения результатов (орел или решка).

Ожидаемые значения подбрасывания монеты - это распределение вероятностей подбрасывания монеты.

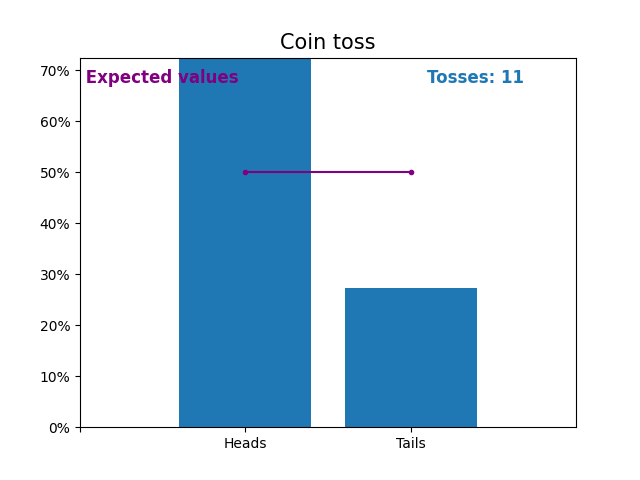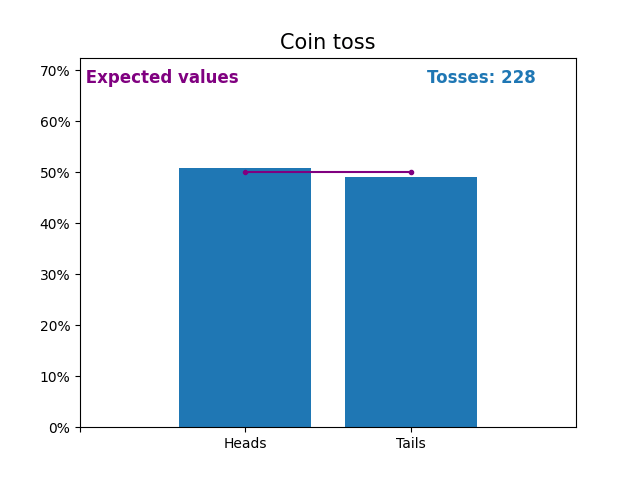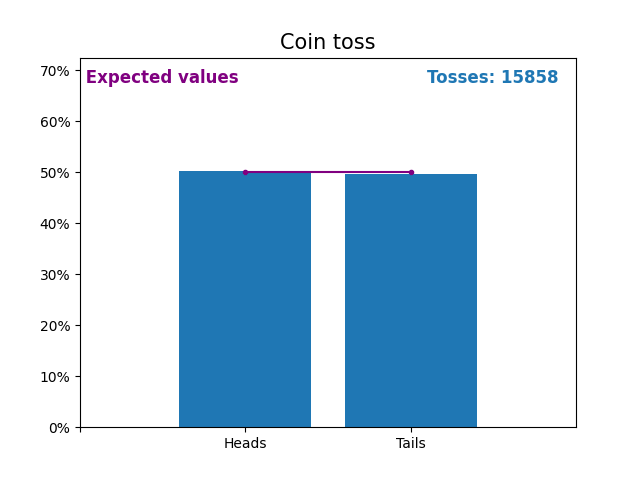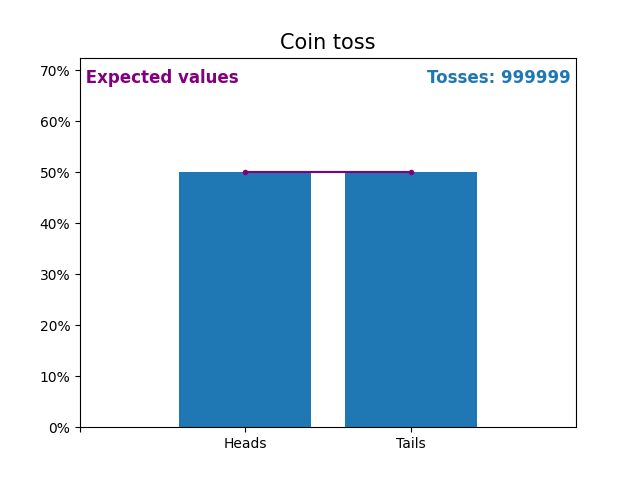
Обратите внимание, как результат случайных подбрасываний монет приближается к ожидаемым значениям (50%) по мере увеличения количества подбрасываний.

Точно так же график, показывающий результаты растущего числа бросков кубиков и ожидаемые значения результатов (от 1 до 6).

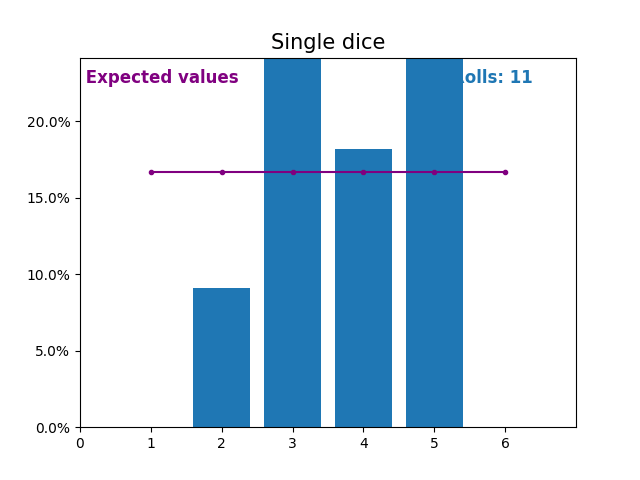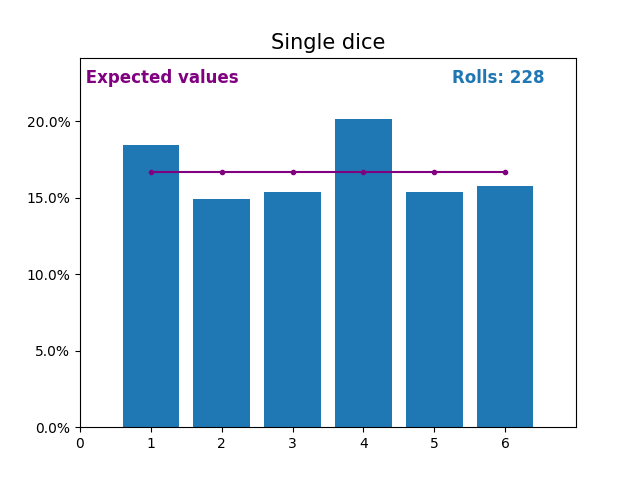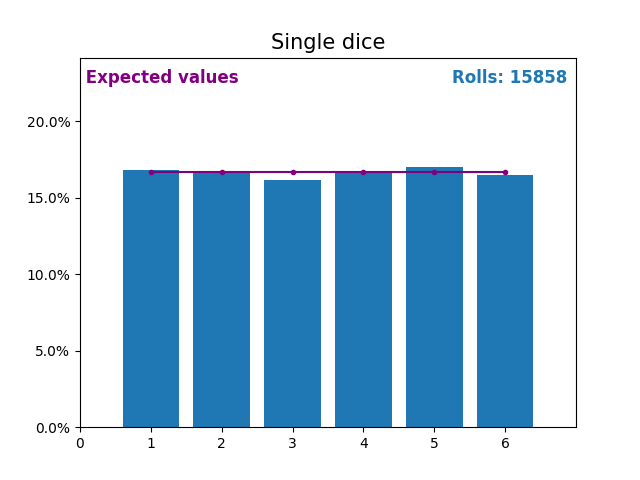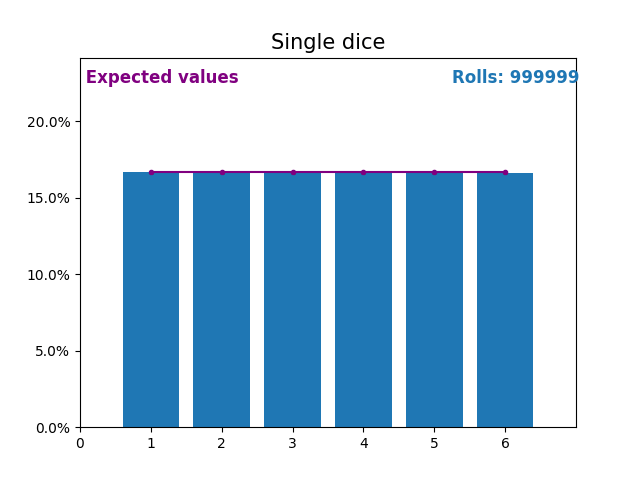
Ещё раз обратите внимание, как результат случайных бросков кубиков приближается к ожидаемым значениям (1/6, или 16,666%) по мере увеличения количества бросков.

Когда случайная величина представляет собой сумму кубиков, результаты и ожидаемые значения принимают другую форму.

Разная форма возникает из-за того, что существует больше способов получить сумму, близкую к середине, чем небольшую или большую сумму.

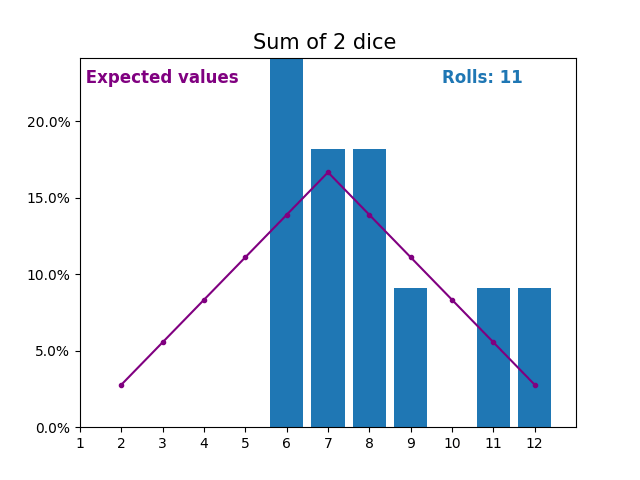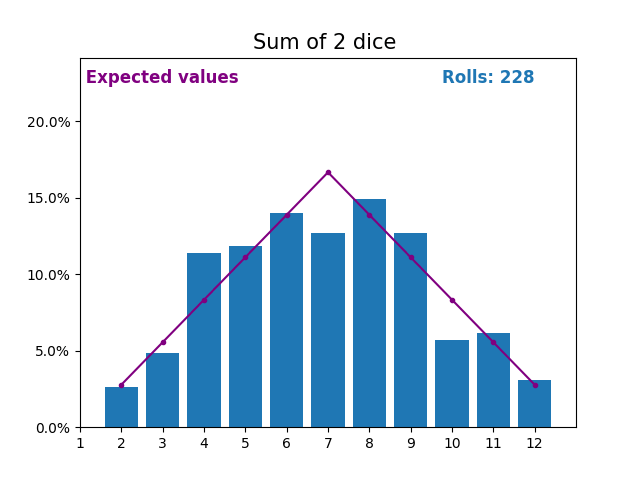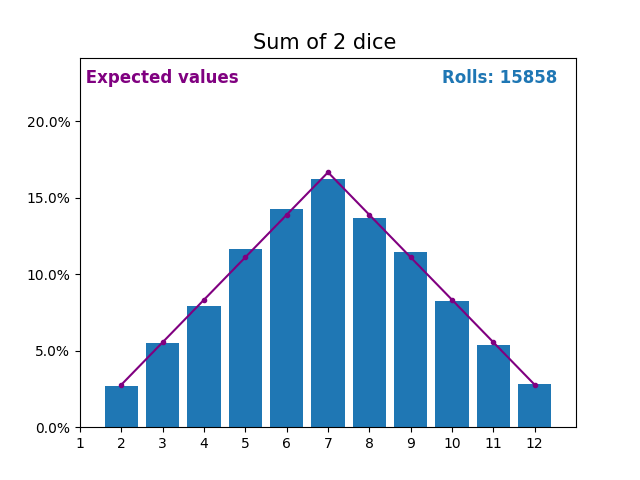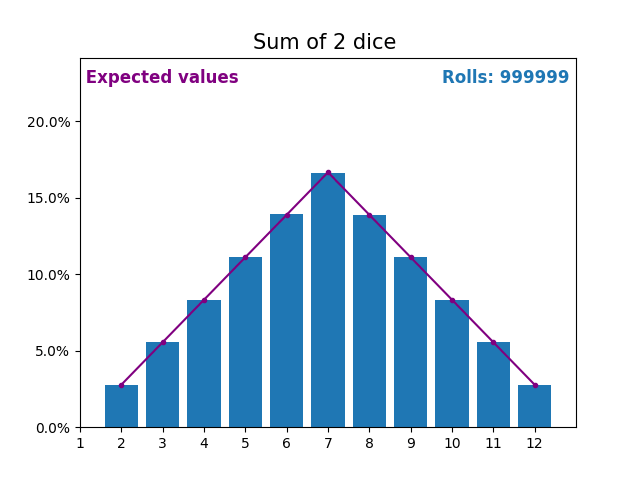
По мере того, как мы продолжаем увеличивать количество кубиков для получения суммы, форма результатов и ожидаемых значений становится все больше и больше похожа на нормальное распределение.

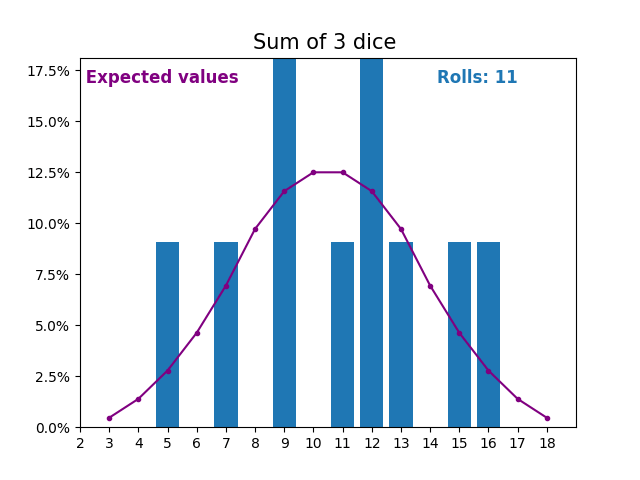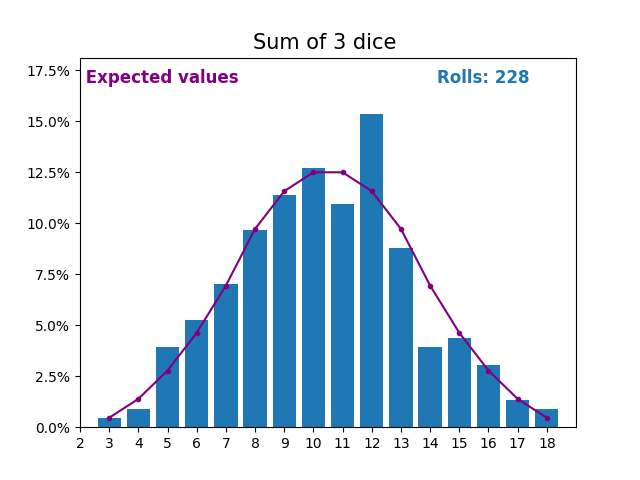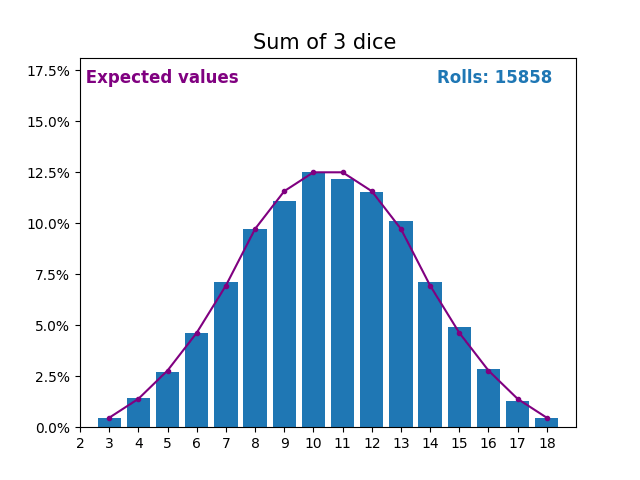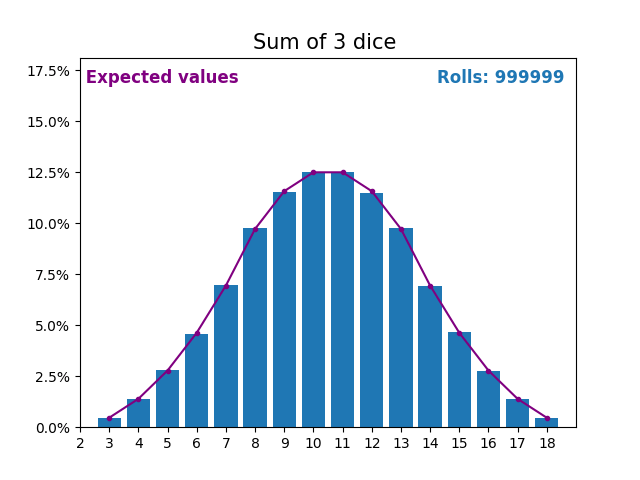
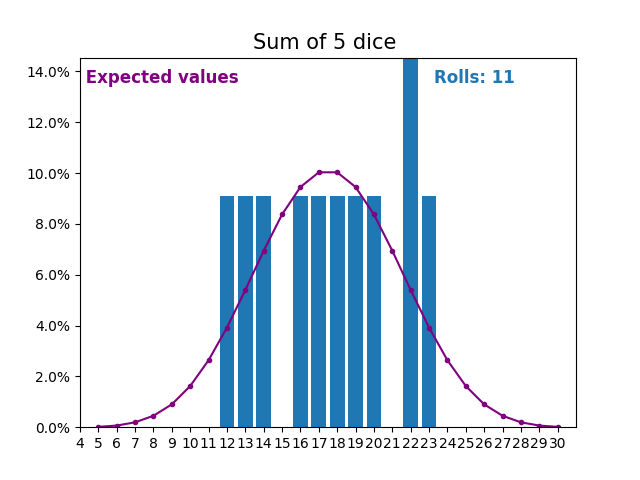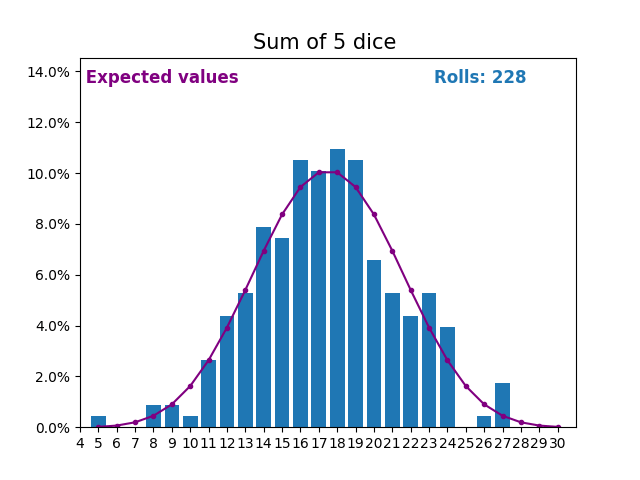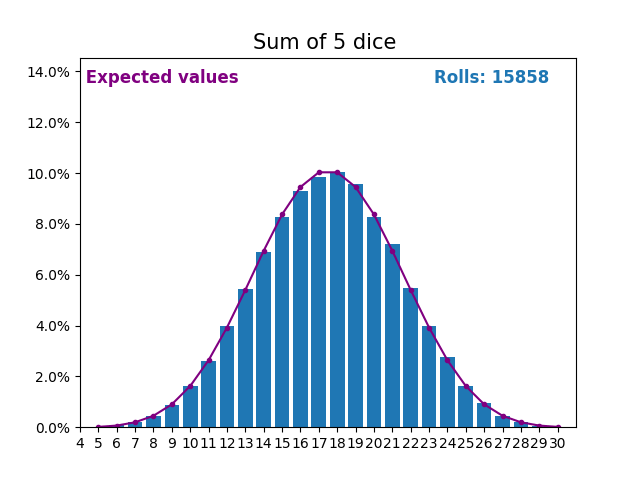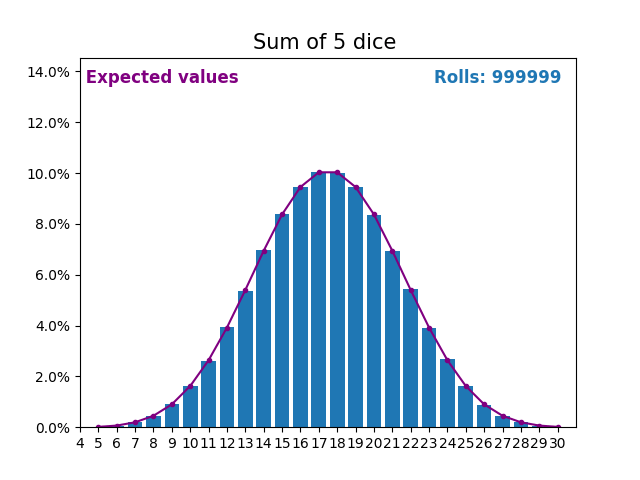
Многие переменные реального мира следуют аналогичному шаблону и, естественно, образуют нормальные распределения.

Обычно распределенные переменные можно анализировать с помощью хорошо известных методов.

На следующих страницах вы узнаете о некоторых из наиболее распространенных и полезных методов.